BAB I. TITIK DAN KURVA PADA SISTEM KOORDINAT CARTESIUS

Assalamu’alaykum...

Hy Guys.. Mau kepoin Geometri Analitik ? Yuk kenalan.. ^_^

Geometri analitik merupakan kajian terhadap obyek-obyek geometri dengan menggunakan sistem koordinat yang diulas menggunakan konsep dan prinsip aljabar dan analisis. Perkembangan geometri analitik dimulai dengan kehadiran bentuk baru persamaan (equation) Bentuk baru persamaan tersebut memungkinkan untuk mengklasifikasikan kurva berdasarkan derajat (degree). Kurva berderajat satu adalah garis lurus (straight lines), kurva berderajat dua merupakan irisan kerucut (conic sections), dan kurva berderajat tiga dinamakan kurva kubik (cubic curves).

Descartes (sekitar tahun 1637) menggunakan bentuk baru persamaan tersebut untuk mengubah masalah-masalah geometri menjadi masalah aljabar menggunakan koordinat sehingga dapat diselesaikan dengan manipulasi aljabar. Pengubahan tersebut dilakukan berdasarkan relasi antara himpunan titik-titik yang berkorespondensi satu-satu dengan himpunan bilangan riil. Sebuah titik dapat dinyatakan sebagai pasangan bilangan riil (x,y). Descartes dalam bukunya Geometry (La Geometrie) menggunakan pertama kali bentuk sumbu koordinat untuk menganalisis sebuah kurva secara aljabar, seperti terlihat dalam gambar berikut.

Kedudukan Titik-titik dan Jarak antara Dua Titik

Sebelum mempelajari kedudukan titik-titik dan jarak antara dua titik, kita kenalan dulu yuk sama titik. Titik ? Apa itu titik ?  perhatikan gambar dibawah ini.

       

Dari 2 gambar diatas kita dapatkan, ciri-ciri titik  :

1. Tidak memiliki panjang, lebar, tinggi,  besaran, satuan.
2. Mempunyai letak/posisi.

Jadi, dapat kita simpulkan bahwa titik adalah bagian terkecil dari suatu objek, yang menempati suatu tempat atau posisi, yang tidak memiliki panjang, lebar, dan tinggi, besaran, sataun .

Titik-titik pada sebuah bidang yang membentuk himpunan titik dan memenuhi suatu kriteria tertentu dinamakan kedudukan titik (locus of points). Kedudukan titik dapat dinyatakan sebagai suatu fungsi. Misalnya titik-titik pada lingkaran berjari-jari 1 cm dapat dinyatakan sebagai x² + y² = 1. Secara geometris, hanya titik-titik berjarak 1 cm dari titik pusat lingkaran tersebut yang memenuhi kedudukan titik yang dinyatakan oleh persamaan x² + y² = 1. Teorema-teorema dasar tentang kedudukan titik-titik (Fundamental Locus Theorems) sebagai berikut.

no	Teorema	Sketsa
1.	Teorema 1.1 Kedudukan titik-titik yang berjarak sama yaitu d dari sebuah titik P adalah sebuah lingkaran berpusat di titik P dengan ukuran panjang jari-jari d
2.	Teorema 1.2 Kedudukan titik-titik yang berjarak sama yaitu d dari sebuah garis l  adalah sepasang garis-garis sejajar yang masing-masing berjarak d dari garis l
3.	Teorema 1.3 Kedudukan titik-titik yang berjarak sama (equidistant) dari dua buah titik P dan Q adalah sebuah ruas garis (disebut perpendicular bisector).yang tegak lurus  terhadap ruas garis  dan membagi  menjadi dua bagian sama besar.
4.	Teorema 1.4 Kedudukan titik-titik yang berjarak sama dari dua garis yang sejajar yaitu l1 dan l2 merupakan sebuah garis diantara keduanya dan sejajar dengan kedua garis tersebut.
5.	Teorema 1.5 Kedudukan titik-titik yang berjarak sama terhadap dua garis yang berpotongan yaitu l1 dan l2, adalaha sepasang ruas garis (disebut bisectors) yang membagi dua sama besar sudut-sudut yang yang dibentuk garis l1 dan l2
6.	Teorema 1.6 Kedudukan titik-titik yang berjarak sama dari kedua sisi sebuah sudut adalah sebuah ruas garis yang membagi dua sudut tersebut (bisector of angle)
7.	Teorema 1.7 Kedudukan titik-titik yang berjarak sama dari dua buah lingkaran konsentris (concentric circles) adalah sebuah lingkaran yang konsentris terhadap kedua lingkaran tersebut dan berada tepat di tengah keduanya
8.	Teorema 1.8 Kedudukan titik-titik pada jarak tertentu dari sebuah lingkaran yang memiliki jari-jari lebih panjang dari jarak tersebut merupakan sebuah pasangan lingkaran konsentris, di mana masing-masing kedudukan titik tersebut berada di salah satu sisi lingkaran pada jarak tertentu tersebut.
9.	Teorema 1.9 Kedudukan titik-titik yang berjarak tertentu dari suatu lingkaran berjari-jari kurang dari jarak tersebut merupakan sebuah lingkaran yang berada di luar lingkaran pertama dan saling konsentris.

CONTOH 
PEMBUKTIAN
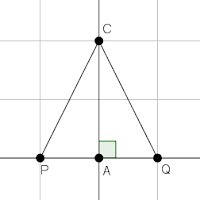
p : Kedudukan titik-titik pada suatu ruas garis berjarak sama dari P dan Q
q : Ruas garis tegak lurus PQ dan membagi PQ menjadi 2 bagian sama panjang

Diketahui :
-Titik P dan titik Q
-Ruas garis AB tegak lurus PQ dan membagi ruas garis PQ
Ditanya : Misalk sembarang titik di AB dalah C, C berjarak sama ke PQ yaitu ?

PENYELESAIAN :

Sistem Koordinat kartesius

Diambil dua buah garis yang tegak lurus sesamanya, yang satu mendatar yang lain tegak lurus padanya, yang mendatar disebut sumbu-x dan tegaklurus disebut sumbu-y. Titik potong kedua sumbu dijadikan titik o (= titik pangkal). Bagian sumbu-x yang terletak sebelah kanannya O diberi tanda positif, dan sebelah kirinya O diberi tanda negatif. Bagian sumbu-y yang letaknya diatas O diberi tanda positif dan dibawahnya O diberi tanda negatif.

Bilangan-bilangan pada sumbu-x disebut absisi atau  koordinat-x. Bilangan pada sumbu-y disebut ordinat atau koordinat-y. Kesemuanya disebut pasangan-pasangan koordinat atau salib sumbu.

Kedua sumbu membagi bidang datar atas 4 bagian :

1. Kuadran I , diatas sumbu-x, sebelah kanannya sumbu-y. 
2. Kuadran II , diatas sumbu-x, sebelah kirinya sumbu-y
3. Kuadran III , dibawah sumbu-x, sebelah kirinya sumbu-y
4. Kuadran IV , dibawah sumbu-x, sebelah kanannya sumbu-y

4.  

Tanda-tanda absis dan ordinat suatu titik adalah sebagai berikut

kuadran	koordinat
	x	y
I	+	+
II	-	+
III	-	-
IV	+	-

  

Dengan cara demikian tiap titik pada bidang dapat ditentukan oleh sepasang bilangan, yang pertama menunjukkan absis dan yang kedua ordinat . sebaliknya tiap pasang bilangan menentukan sebuah titik pada bidang.

JARAK ANTARA DUA TITIK

Selanjutnya, kita belajar bagaimana menghitung jarak antara dua titik yang berbeda posisi. Kita dapat mengikuti langkah-langkah berikut: 

1. Buatlah dua titik berbeda yaitu A dan B lalu hubungkan dengan sebuah ruas garis.
2. Buat sebuah garis melalui A dan sebuah garis lain yang melalui B sehingga kedua garis berpotongan tegak lurus.
3. Tentukan titik potong kedua garis yaitu C sehingga diperoleh segitiga siku-siku ACB atau BCA lalu ukur panjang ruas garis CA dan CB
4.  Tentukan panjang ruas garis AB dengan menggunakan Teorema Phytagoras :   

Ada juga nih langkah-langkah menghitung titik tengah antara dua titik atau suatu ruas garis :

1. Buatlah dua titik berbeda yaitu A dan B lalu hubungkan dengan sebuah ruas garis.
2. Tentukan titik tengah dari yaitu
   
   
    Jadi titik tengah dari  adalah
   
   

Contoh:

Jika titik tengah dari titik A(5,7) dan B(3,9) adalah titik C( , ) maka titik C adalah

Penyelesaian :

Jadi titik tengah dari  adalah C (4,8)