BAB III. KURVA BERDERAJAT DUA (LINGKARAN)

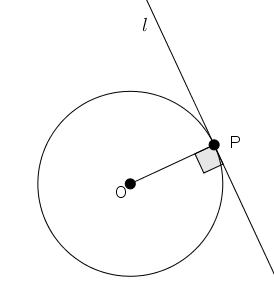
LINGKARAN

Lingkaran : Himpunan titik-titik (pada bidang datar) yang jaraknya dari suatu titik tertentu sama panjang

Persamaan Kurva Berderajat Dua :

Ax² + By² + Cx + Dy + Ey + F = 0, A dan B ≠ 0

Kedudukan titik-tik yang bergerak dengan rasio jarak tertentu dari sebuah titik tetap dan garis tetap akan membentuk irisan kerucut (conic section)

Esentrisitas : Perbandingan Tetap

Direktriks   : Garis Tetap

Titik Fokus

Esentrisitas : e = d : d'

d = d'  ⇒ e = 1

d < d'  ⇒ e < 1

d > d'  ⇒ e > 1

Lingkaran dengan titik pusat C (a, b), jari-jari r, dan ada titik pada lingkarang P(x, y)

Konsep Jarak : 

CP = r = √( x - a )² + ( y - b )² 

(x - a)²  + (y – b)²  = r² 

x²  – 2ax + a²  + y²  – 2by + b² = r²

x² – 2ax + y² – 2by + a² + b² – r² = 0

A = 1, B = 1, C = 0, D = -2a, E = -2b, F = a + b – r

Persamaan umum lingkaran (x - 2) + (y – b) = r

Contoh 1 :

Jika lingkaran berpusat di (0, 0) dengan r = 3

Penyelesaian :

(x - a)² + (y – b)² = r²

(x - 0)² + (y – 0)² = 3²

x² + y² = 9

Contoh 2 : 

Misalkan lingkaran mempunyai titik (5, 1) berpusat di (-1, 0). Tentukan jari-jari dari lingkaran tersebut

Penyelesaian :

Jadi persamaan lingkarannya :

(x + 1)² + (y – 0)² = √37²

(x + 1) + y² = 37

Persamaan Lingkaran :

x²  + y² - 2ax  – 2by + c = 0

dengan

c = a² + b² – r²

Apakah yang terjadi jika c = 0, c > 0 dan c < 0 ??

1. Jika c = 0, maka a² + b² = r²

(x - a)² + (y – b)² = a² + b²

x² – 2ax + y² – 2by + a² + b² = a² + b²

x² – 2ax + y² – 2by = 0

x² + y² – 2ax– 2by = 0

jika berpusat di (0, 0), maka lingkaran yang terbentuk mempunyai jari 0

           2.  Jika c > 0, maka a² + b² > r²

           3.  Jika c < 0, maka a² + b² < r²

         Ingat !!

          c = a² + b² – r² ⇔ a² + b² – c = r² ⇔ r = √(a² + b² - c)

a.       r > 0 ⇔ √(a² + b² - c) > 0 (riil)

b.      r< 0 ⇔  √(a² + b² - c) < 0 (Tidak riil)

Jadi, agar lingkaran riil maka √(a² + b² - c)  > 0

Garis Singgung Antara 2 Lingkaran

1. Garis Singgung persekutuan dalam lingkaran

   Garis Singgung persekutuan dalam lingkaran adalah garis singgung 2 lingkaran yang memotong garis 2 titik pusat

2. Garis Singgung persekutuan luar lingkaran

   Garis Singgung persekutuan luar lingkaran adalah garis singgung 2 lingkaran yang tidak memotong garis 2 titik pusat

Sudut antar 2 lingkaran yang berpotongan

Contoh Soal :

Tentukan persamaan garis singgung lingkaran x + y = 25 yang sejajar garis y = 2x + 3

1. Identifikasi masalah

-      x² + y² = 25 ( merupakan persamaan lingkaran), maka didapatkan sebuah lingkaran dengan titik pusat (0,0) dan jari-jari 5

-       garis singgung sejajar dengan garis y = 2x + 3, didapatkan m = 2

-       misalkan garis singgung lingkaran adalah k dan garis y = 2x + 3 adalah h

-       k // h, maka mk = mh = 2

-       k = y = 2x + 3, data yang dibutuhkan titik singgung untuk mencari c

       2. Strategi pemecahan masalah

mencari titik singgung

P₁ dan P₂ pada lingkarang maka :

x₁² + y₁² = 25

x₂² + y₂² = 25

P₁ dan P₂ pada garis singgung

y₁ = 2x₁ + c

y₂ = 2x₂ + c

Substitusikan persamaan y = 2x + c dan x₁² + y₁² = 25
x² + (2x + c )² = 25

x² + 4x² + 4xc + c² = 25
5x² + 4cx + c² = 25

5x² + 4cx + c² - 25 = 0

a= 5, b= 4c, c =  c² - 25
Agar memiliki solusi riil, syarat garis singgung adalah D = 0
b² - 4ac = 0
(4c)² - 4 (5) ( c² - 25 ) = 0
16c² - 20c² + 500 = 0 
-4c² + 500 = 0 

500 = 4c²

125 = c²
c ± 5√5

Jadi, persamaan garis singgungnya  :

y = 2x - 5√5

dan 

y = 2x + 5√5

Jika diketahui garis y = mx + n dan lingkaran x² + y² = r² maka persamaan garis singgung yang sejajar y = mx + h yaitu y = mx + k dimana k = ± r √(1+m²)
Sehingga diperoleh 2 garis singgung 

y = mx + r √(1+m²)

dan 

y = mx - r √(1+m²)

Contoh Soal :

Diketahui :
Persamaan ( x - 2 )² + ( y - 3 )² = 16

Ditanya : 
Apakah A(5,-4) berada didalam, diluar atau pada lingkaran ?

Penyelesaian :

Titik (5,-4) 

( x - 2 )² + ( y - 3 )² = 16

( 5 - 2 )² + ( -4 - 3 )² = 16

9 + 49 = 16

58 > 16

Ternyata jarak titik A > jari-jari lingkaran.

Berarti titik berada di luar lingkaran.

Titik pusat (0,0) : y = mx + r √(1+m² )

titik pusat ditranslasikan ke (a, b)

(y - b ) = m ( x - a ) + r √(1+m² )

y = mx - am + b + r √(1+m² )

Contoh : jika persamaan lingkaran x²  + y²  = 25 dengan titik pusat (0,0) ditranslasikan ke (2,3) 

y = 2x -2.2 + 3 + 5√5

   = 2x -4 + 3 + 5√5

   = 2x - 1 + 5 √5

Menggunakan Geogebra

Persamaan Lingkaran	Garis Singgung	Titik Singgung	Titik Pusat
x2  + y2  = 25	y = 2x + 11.18	(-4.47, 2.24)	(0, 0)
(x-2)2  + y2  = 25	y = 2x + 7.18	(-2.47, 2.24)	(2, 0)
(x-2)2  + (y-3)2  = 25	y = 2x + 10.18	(-2.47, 5.24)	(2, 3)

Tali busur adalah garis yang memotong lingkaran

Tali busur singgung adalah garis yang menguhubungkan 2 titik singgung

Persamaan garis kutub

Diketahui persamaan lingkaran x² + y² = r² dari titik (x₀, y₀) dapat dibuat 2 garis singgung S₁ (x₁, y₁) dan S₂ ( x₂, y₂).

Maka garis S₁ dan S₂  disebut tali busur singgung yaitu garis yang menghubungkan 2 titik singgung, maka persamaan garis kutub B(x₀, y₀) terhadap x² + y² = r²  adalah

x₀x + y₀y = r²  

sifat garis kutup tersebut adalah

1. menghubungkan 2 titik singgung dari garis-garis singgung yang berpotongan di (x₀, y₀)
2. tegak lurus terhadap garis yang menghubungkan (x₀, y₀) dari titik pusat lingkaran

garis singgung h1 dan h2 berpotongan di Q

A titik singgung h1

B titik singgung h2

AB ⊥ PQ

AB garis kutub = x₀x + y₀y = r²  brlaku jika persamaan lingkaran x² + y² = r²

BAB II. GARIS SEBAGAI KURVA BERDERAJAT SATU

Titik Diskrit

Titik Kontinu

2.1       Persamaan Umum Garis, Gradien dan Sudut Inklinasi

Ax + By + C = 0 untuk A, B, C bilangan riil dan x, y variabel bilangan riil

Contoh 1

Sebuah garis yang melalui titik A(1, 2), B(-3, 4), dan C(5, 0) maka persamaan kurva berderajat satu untuk garis tersebut ditentukan sebagai berikut.

Langkah 1) 

Substitusi koordinat titik ke dalam persamaan kurva

Garis melalui A(1, 2) ⇒A(1) + B(2) + C = 0 ⇒ A + 2B + C = 0 ---------- pers. 1

Garis melalui B(-3, 4) ⇒ A(3) + B(-4) + C = 0 ⇒ -3A + 4B + C = 0 ----- pers. 2

Garis melalui C(5, 0) ⇒ A(5) + B(0) + C = 0 ⇒ 5A + C = 0 -------------- pers. 3

Langkah 2) 

Membuat sistem persamaan linier tiga variabel 

−𝐴+2𝐵+𝐶=03𝐴+4𝐵+𝐶=05𝐴+𝐶=0

Langkah 3) 

Menyelesaikan sistem persamaan linier

Penyelesaian sistem persamaan linier di atas yaitu :

A = 1, B = 2 dan C = -5

Maka persamaan kurva berderajat satu untuk garis yang melalui A(1, 2), B(-3, 4), dan C(5, 0) yaitu x + 2y - 5 = 0

Sketsa garis tersebut pada sistem koordinat Cartesius seperti gambar di atas.

Garis x + 2y - 5 = 0 seperti ditunjukkan pada gambar di atas membentuk sudut terhadap sumbu x positif. Besarnya sudut yang terbentuk tersebut akan mempengaruhi kemiringan garis. Sudut bernilai positif yang dibentuk antara garis dan sumbu x positif dinamakan sudut inklinasi garis (angle of inclination) dan biasanya dinotasikan oleh sudut α. Kemiringan suatu garis dinamakan gradien (slope of the line) dan dinyatakan oleh notasi m.

MENDESKRIPSIKAN GARIS BERDASARKAN GRADIEN DAN SUDUT INKLINASI

OR ⊥ AB, sehingga 

Tabel 1. Hubungan antara gradien, sudut inklinasi, dan bentuk garis

Nilai Gradien (m)	Nilai sudut inklinasi (α)	Deskripsi bentuk garis
m > 0	sudut lancip	Dari kiri bawah ke kanan atas ( / )
m = 0	α = 0०	Mendatar, sejajar sumbu x (­一)
m < 0	sudut tumpul	Dari kiri atas ke kanan bawah ( \ )

2.2 Sifat-sifat Garis dalam Bidang : Kesejajaran dan Perpotongan

         Sifat-sifat garis yang berada dalam sebuah bidang dalam geometri Euclide meliputi garis-garis yang berpotongan atau tidak berpotongan. Dua buah garis dikatakan berpotongan jika ada sebuah titik potong yang dilalui kedua garis. Dua garis tidak berpotongan disebut saling sejajar.

Contoh Soal :

Dua buah garis m dan n berpotongan di titik (-1, 3) dan membentuk sudut 30०. Tentukan persamaan kedua garis tersebut.

Penyelesaian :

Diketahui : A (-1,3), 

                      Garis m dan n berpotongan

                 sudut berpotongan : 30०

Ditanya : Persamaan kedua garis m dan n

Jawab:

Titik potong di (0,0)

 Garis n1

Persamaan dengan titik (-3,2) dan m = 7

Garis n2

Persamaan dengan titik (-3,2) dan m = -1

2.3 Persamaan Normal Sebuah Garis

x cos 𝛃 + y sin 𝛃 - p = 0

dengan, 

Contoh soal

     Misalkan x menyatakan suhu dalam derajat Celsius (centigrade) dan variabel y menyatakan suhu dalam derajat Fahrenheit. Ukuran suhu 0°C setara dengan 32°F, dan suhu 100°C sama dengan 212°F. Tentukan persamaan garis yang menyatakan hubungan suhu y Fahrenheit terhadap suhu x Celsius dalam bentuk y = mx + c. Ubahlah persamaan tersebut dalam persamaan normal. Buatlah grafik garis pada sistem koordinat Cartesius, tentukan titik-titik potong garis dengan sumbu koordinat.

Penyelesaian :

Diketahui :
x menyatakan suhu dalam derajat Celsius
y menyatakan suhu dalam derajat Fahrenheit
0°C setara dengan 32°F
suhu 100°C sama dengan 212°F

Ditanya :
1. Persamaan garis 
2. Persamaan normal garis tersebut.
3. grafik garis pada sistem koordinat Cartesius.

Jawab :

1. Persamaan Garis

   Menggunakan persamaan gradien

2) Persamaan Normal garis tersebut

 y = 1,8x + 30, maka m = 1,8

𝛂 = arc tan m

𝛂 = arc tan 1,8

𝛂 = 60,95◦

𝛃 = 90° + 60,95°

𝛃 = 150,95°

Misalkan titik potong di y = 0, maka x = -16,67

p = -16,67 . cos 150,95°

p = -16,67 . -0,87

p = 14,5 

Persaam Normal garis :

x cos 𝛃 + y sin 𝛃 - p = 0

x cos 150,95° + y sin 150,95° - 14,5 = 0

x (-0,87) + y (0,48) - 14,5 = 0

-0,87x + 0,48y - 14,5 = 0

Jadi persamaan normal dari  y = 1,8x + 30 adalah -0,87x + 0,48y - 14,5 = 0

3) Grafik