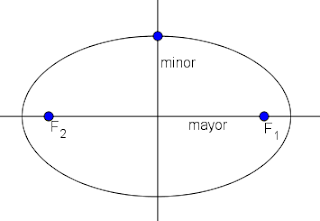
A. Ellips
Ellips adalah himpunan semua titik yang jumlah jaraknya terhadap dua titik tertentu tetap besarnya. untuk setiap titik T berlaku |TF₁| + |TF₂| = 2a
Titik F₁ dan F₂ disebut titik apu atau fokus.
AB disebut sumbu panjang : |AB| = 2a
CD disebut sumbu pendek
Titik-titik A, B, C dan D disebut puncak-puncak ellips.
|TF₁| + |TF₂| = PQ = 2a
Kedua ruas dikuadratkan :
Kedua ruas dikuadratkan lagi :
Karena a > 0 maka a² - c² > 0 maka a² - c² = b²
Hasilnya,
Persamaan Ellips diatas adalah
Dan
Persamaan untuk Ellips diatas adalah
B. HYPERBOLA
Hiperbola adalah himpunan titik-titik pada suatu bidang dimana selisih jarak titik terhadap dua titik fokusnya (F₁ dan F₂) konstan
|PF₁| − |PF₂| = ± 2a
c² = a² + b²
Hiperbola 1
Memiliki fokus (±c, 0) dimana c² = a² + b², titik puncak (±a, 0) dan asimtoot nya adalah y = ± (b/a)x
Hiperbola 2
Memiliki fokus (0, ±c) dimana c² = a² + b², titik puncak (0, ±a) dan asimtoot nya adalah y = ± (a/b)x
C. PARABOLA
Parabola adalah himpunan titik-titik yang berjarak sama dari suatu titik dan suatu garis tertentu.
Gambar 1
Gambar 2
Gambar 3
Jika sumbu simetri berimpit dengan sumbu y, titik puncak parabola berimpit dengan titik asal tetapi parabolanya terletak di setengah bidang sebelah atas (Gambar 4) maka persamaan parabolanya adalah x²= 2py
Gambar 4
Jika sumbu simetri berimpit dengan sumbu y, titik puncak parabola berimpit dengan titik asal tetapi parabolanya terletak di setengah bidang sebelah bawah (Gambar 5) maka persamaan parabolanya adalah x²= -2py












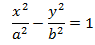

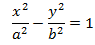











Tidak ada komentar:
Posting Komentar